Elektronický vzdelávací materiál

Smernicová rovnica priamky v rovine

Smernicová rovnica priamky vychádza z poznatku, že priamka je v rovine jednoznačne určená bodom a smerovým uhlom.

Smerový uhol priamky p, ktorá je rovnobežná s osou x, je nulový.

Smerový uhol priamky p rôznobežnej s osou x, je konvexný uhol, ktorého vrchol je priesečník P priamky p s osou z, jedno jeho rameno je tá časť priamky p, ktorá obsahuje iba body s nezápornou y-ovou súradnicou.

Druhé rameno je tá časť osi z, ktorej prienik s kladnou polosou x je polpriamka (obr. 3.97, 3.98).

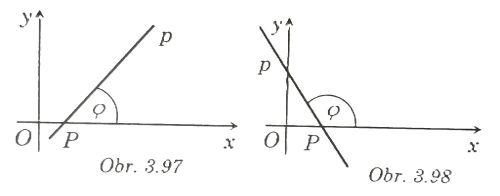
Smernica priamky p rôznobežnej s osou y je číslo k = tan φ .

Priamka p rovnobežná s osou y nemá smernicu, lebo jej smerový uhol je 90° a tan 90° nie je definovaný.

Budeme hľadať analytické vyjadrenie priamky p, ktorá je určená bodom A[a{1}, a{2}] a smernicou k (obr. 3.99). Pre ľubovoľný bod X[x, y] v rovine platí:

Každá priamka rôznobežná s osou y má rovnicu tvaru y = kx + q kde k,q ∈ R. Nazýva sa smernicová rovnica priamky.

Ak do smernicovej rovnice y = kx + q dosadíme x = 0 dostaneme y = k * 0 + q = q čo znamená, že bod [0, q] leží na priamke aj na osi y.

Teda koeficient q určuje priesečník priamky s osou y. Priamky rovnobežné s osou y nemajú smernicovú rovnicu, lebo nemajú smernicu.